要約
目的： 飲用牛乳取引における「酪農協」対「メーカー」（＝生処間）および「メーカー」対「スーパー」（＝処販間）の関係は、双方がある程度の寡占的価格形成力をもつ「双方寡占」の可能性が高い。しかし、近年ではスーパーの価格形成力が突出し、メーカーがますます低価格を強いられ、そのしわ寄せによって、生乳生産者が安すぎる乳価を引き受けているというのが酪農協の主張である。しかし、これらの関係を実証した計量分析は、我々の知る限り存在しない。もし、生処販の価格形成力のバランス（＝垂直的パワー・バランス）を定量的に明らかにできれば、いかに役立つであろうか。垂直的パワー・バランスがちょうど拮抗した場合の価格水準を、一種の「適正価格」の指標として提示し、取引コストの節約に貢献することも期待されよう。本研究では、現状乳価を形成している生処間および処販間の垂直的パワー・バランスを推計し、それらのパワーがちょうど拮抗した場合の価格水準の試算方法を示すことを目的とする。
調査研究経緯： 酪農協の価格形成力（＝水平的競争度）に関する実証研究については、鈴木宣弘「推測的変動による不完全競争市場のモデル化と政策変更効果の計測−生乳市場を事例として−」（『農業経済研究』第63巻1号、1991年）を端緒とする鈴木らの一連の蓄積があるが、いずれのモデルもメーカー側をプライス・テイカーと仮定し、双方寡占の可能性は組み込まれていなかった。実は、モデルの解が一意に定まらない問題から、双方寡占の実証的研究は、まだ国内外で緒に就いたばかりである。その中で、我々の研究課題に一つの分析フレームワークを与えてくれるのが、米国の肉牛肥育農家とパッカーとの垂直的パワー・バランスに関するAzzam, A.M. "Estimating the Degree of Dominance in a Bilateral Oligopoly"（Applied Economics Letters 3, 1996年）のモデルである。このAzzamの考え方と鈴木らの研究蓄積とを結合し、日本の生処販3者間における垂直的パワー・バランスおよび水平的競争度の推計モデルを構築する。
結論： モデル推計の結果、処販間の垂直的パワー・バランスは、ほぼ0対1であり、スーパーがメーカーに対して圧倒的に優位であるが、スーパー間の水平的競争度は、ほぼ完全競争に近い状態であることが示された。つまり、スーパーは、スーパー間の激しい競争にさらされているにもかかわらず、メーカーに対しては圧倒的パワーを行使している。一方、生処間の垂直的パワー・バランスは、ほぼ対等の0.5対0.5か、酪農協が劣位であり、最小でほぼ0.1対0.9となることが示された。以上の結果は、牛乳取引関係者の多くがもつ実感とも一致しており、興味深い。ただし、垂直的パワー・バランスと水平的競争度との関係の理論的解釈について、まだ検討すべき問題も残っているため、今回の推計値とその解釈は暫定的なものと考え、一層の検討を加えた上で、「適正価格」についても今後の研究で提供したいと考えている。
１．研究課題
飲用牛乳取引における「酪農協」対「メーカー」（＝生処間）および「メーカー」対「スーパー」（＝処販間）の関係は、広域合併や資本集中等により、取引当事者の双方がある程度の寡占的価格形成力をもつ「双方寡占」の関係である可能性が高い。双方寡占の場合に形成される取引価格は、自己に有利な価格を双方が主張するが、最終的に双方がいくらかは譲歩し、折り合った価格水準であると考えられる。しかし、近年のスーパーマーケット・チェーンの成長・上位集中化にともなって、スーパーの価格形成力が突出して強まり、メーカーがますます低価格を強いられていることが、多くの取引関係者によって指摘されるようになってきた。また、そのしわ寄せによって、生乳生産者が安すぎる乳価を引き受けているというのが酪農協の主張である。しかし、本当にスーパーの価格形成力が強いのか、メーカーと酪農協ではどちらが強いのか、を検証した計量経済学的研究は、我々の知る限り存在しない。もし、生処販の価格形成力のバランス（＝垂直的パワー・バランス）を、現状価格との関係とともに定量的に明らかにすることができれば、いかに役立つであろうか。各段階の垂直的パワー・バランスがちょうど拮抗した場合に形成される価格水準を、一種の「適正価格」の指標として取引関係者に提示し、取引コストの節約に貢献することも期待されよう。
そこで、本稿では、日本の現状の飲用乳価や飲用牛乳価格を形成している生処間および処販間の垂直的パワー・バランスを推計し、それらのパワーがちょうど拮抗した場合の価格水準の試算方法を示す。
２．モデル
（１）Azzamモデルのフレームワーク
酪農協の価格形成力（＝水平的競争度）に関する実証研究は、鈴木(1991)を端緒とする鈴木らの一連の蓄積がある（鈴木, 2002）。しかし、いずれのモデルも、買い手側であるメーカーをプライス・テイカーと仮定しており、双方寡占の可能性は組み込まれていなかった。実は、モデルの解が一意に定まらない問題から、双方寡占の実証的研究は、まだ国内外で緒に就いたばかりである。その中で、垂直的パワー・バランスを推計するという本稿の課題に一つの分析フレームワークを与えてくれるのが、米国の肉牛肥育農家とパッカーとの垂直的パワー・バランスの推計モデルを提示したAzzam(1996)の研究である。
このAzzamモデルの枠組みを、ここでは、酪農協とメーカーとの飲用原料乳取引のケースに置き換えて説明する。まず、双方寡占ではなく、酪農協かメーカーかどちらか一方だけが価格形成力をもち、他方がプライス・テイカーである状況を考えてみる。もし価格形成力をもつのが酪農協側であれば、酪農協に最も有利な価格、すなわち市場での最高価格（PFU）で取引されるはずである。逆に、メーカー側だけが価格形成力をもつならば、市場での最低価格（PFL）で取引されるはずである。一方、双方寡占の状況とは、自己に有利な価格を双方が主張するが、最終的に双方がいくらかは譲歩し、取引価格が決められる状況であるから、双方寡占の場合に形成される取引価格は、PFU とPFLの間にあると考えられる。すると、現実の取引価格（PF）は、加重平均価格としてPF = w PFU + (1-w) PFL，
と表現できる。このウエイトwを、酪農協の乳業メーカーに対する垂直的パワーの指標と見なすのである。もし一方が完全優位（他方がプライス・テイカー）であればw=1または0となり、対等であればw=0.5となる。ここで、PFUの形成には、酪農協間の水平的競争度が考慮され、PFLの形成には、メーカー間の水平的競争度が考慮される。水平的競争度は
によって表され、もし完全競争状態であればq=0、完全独占あるいは完全協調の状態であればq=1となる。本稿では、以上のAzzamの考え方を鈴木らの研究蓄積と結合させ、日本の生処販3者間における垂直的パワー・バランスおよび水平的競争度の推計モデルを構築する。
（２）理論モデル
まず、酪農協の価格設定行動を定式化する。日本の生乳市場では、酪農協により飲用原料乳市場と加工原料乳市場の間で用途別差別価格が形成され、個々の酪農家は、酪農協が支払うプール乳価を所与として生乳生産を行っている。この関係をSuzuki
et al. (1993) にならって定式化すると、酪農協がメーカーに対して完全優位な垂直的パワーをもつ場合、飲用原料乳と加工原料乳の2市場間における酪農協の売上高最大化条件より、
(1) PF (1 - θf/ηf)
= PM + TC
が成り立つ。ここで、PFは飲用乳価、PMは加工原料乳価、TCは国内最大の余乳地帯である北海道から最大の消費地である東京への輸送コスト、ηfは酪農協が直面する乳業メーカーの飲用原料乳需要の価格弾力性（絶対値）、θfは飲用原料乳市場における酪農協間の水平的競争度パラメター
である。(1)式で形成される飲用乳価PFは、酪農協対メーカーの垂直的パワー・バランスを1:0と仮定しているため、市場での最高水準となっている。よって、これをPFUと表記し、(1)式を書き換えると、
(2) PFU = (PM + TC) / (1 - θf/ηf).
つぎに、メーカーの価格設定行動を定式化する。メーカーが酪農協およびスーパーに対して完全優位な垂直的パワーをもつ場合、メーカーの利潤最大化条件より、
(3) PW (1 - θw/ηw)
= PF (1 + λw/εw)
+ MCw
が成り立つ。ここで、PWは飲用牛乳の卸売価格、MCw はメーカーの飲用牛乳製造・卸売販売の限界費用、ηwはメーカーが直面するスーパーの飲用牛乳需要の価格弾力性（絶対値）、θwは飲用牛乳卸売市場におけるメーカーの水平的競争度パラメター
、εwはメーカーが直面する酪農協の飲用原料乳供給の価格弾力性、λwは飲用原料乳市場におけるメーカーの水平的競争度パラメター
である。(3)式で形成される飲用牛乳卸売価格PWは、メーカー対スーパーの垂直的パワー・バランスを1:0と仮定しているため、市場での最高水準PWUと表記できる。また、同式で形成される飲用乳価PFは、酪農協対メーカーの垂直的パワー・バランスを0:1と仮定しているため、市場での最低水準PFLと表記できる。よって、(3)式を書き換えて、
(4) PFL = [PWU
(1 - θw/ηw)
- MCw] / (1 + λw/εw),
(5) PWU = [PFL
(1 + λw/εw)
+ MCw] / (1 - θw/ηw).
続いて、スーパーの価格設定行動を定式化する。スーパーがメーカーおよび消費者に対して完全優位な垂直的パワーをもつ場合、スーパーの利潤最大化条件より、
(6) PR (1 - θr/ηr)
= PWL (1 + λr/ηr)
+ MCr
が成り立つ。ここで、PRは飲用牛乳の小売価格、MCrはスーパーの飲用牛乳小売販売の限界費用、ηrはスーパーが直面する消費者の飲用牛乳需要の価格弾力性（絶対値）、θrは飲用牛乳小売市場におけるスーパーの水平的競争度パラメター
、εrはスーパーが直面するメーカーの飲用牛乳供給の価格弾力性、λrは飲用牛乳卸売市場におけるスーパーの水平的競争度パラメター
である。(6)式で形成される飲用牛乳小売価格PRは、スーパー対消費者の垂直的パワー・バランスを1:0と仮定しているため、市場での最高水準であるが、これを現実の飲用牛乳小売価格と見なす。また、同式で形成される飲用牛乳卸売価格PWは、メーカー対スーパーの垂直的パワー・バランスを0:1と仮定しているため、市場での最低水準PWLと表記できる。よって、(6)式を書き換えると、
(7) PWL = [PR (1 - θr/ηr)
- MCr] / (1 + λr/εr).
以上の(2)、(4)、(5)、(7)式を利用して、現実の取引価格を、市場での最高水準と最低水準との加重平均価格として表現する。まず、現実の飲用乳価をPFは、酪農協のメーカーに対する垂直的パワー・パラメター
を導入して、
(8) PF = ωｆ PFU
+ (1-ωｆ) PFL
または
(9) PF = ωｆ (PM + TC) / (1 - θf/ηf)
+ (1 - ωｆ) [PWU
(1 - θw/ηw)
- MCw] / (1 + λw/εw).
一方、現実の飲用牛乳卸売価格PWは、メーカーのスーパーに対する垂直的パワー・パラメター
を導入して、
(10) PW = ωw PWU
+ (1 - ωw) PWL
または
(11) PW = ωw [PFL
(1 + λw/εw)
+ MCw] / (1 - θw/ηw)
+ (1 - ωw) [PR (1 - θr/ηr)
- MCr] / (1 + λr/εr).
(9)式および(11)式には共通するパラメターが含まれているので、両式のパラメター制約下で、垂直的パワー・パラメター（ωｆ，ωw）および水平的競争度パラメター（θf，θw，θr，λw，θr）が同時決定される。
しかし、実証分析を行う際は、PWUおよびPFLが観測不可能な変数であるため、(9)および(11)式を同時方程式モデルとして用いることはできない。そこで、パラメター値にいくつかの仮定を設け、両式を別個に取り扱う推計方法を以下に示す。
（３）実証モデル
まず、メーカー対スーパーの関係を表す(11)式について、つぎの仮定を設ける。
(1)一般に、日本の乳業メーカーは酪農協に対して圧倒的に強い垂直的パワーをもつと言われているので、ひとまず酪農協対メーカーの垂直的パワー・バランスを0:1と仮定し、現実の飲用乳価を市場の最低水準と見なすことは妥当であろう。よって、(11)式のPFLをPFに置き換える。
(2) λwとθwは、どちらもメーカーの水平的競争度パラメターであり、λrとθrは、どちらもスーパーの水平的競争度パワー・パラメターである。よって、λw=θw，λr=θrと仮定する。
(3) 飲用原料乳か飲用牛乳かに関わりなく、その供給の価格弾力性は、メーカーとスーパーいずれにとっても同一と仮定し、εw=εr≡εと置き換える。需要の価格弾力性も、メーカーとスーパーいずれにとっても同一と仮定し、ηw=ηr≡ηと置き換える。なお、εおよびηの値はAzzamと同様に定数と仮定する。
(4) メーカーの費用関数をC = Vq + F，Cは総費用、Vは変動費単価、Fは固定費、qは飲用牛乳供給量と仮定する。この場合、メーカーの限界費用MCwは変動費単価Vに等しくなる。一方、スーパーの限界費用MCrについては、飲用牛乳小売販売に係る費用の大半は固定費と考えられるため、MCr=0と仮定する。
以上の仮定(1)〜(4)を(11)式に組み込むと、
(12) PW = ωw [PF (1 + θw
/ω) + V] / (1 - θw/η) + (1 - ωw)
PR (1 - θr/η) / (1 + θr
/ε)
または
(13) PW = ωw (1 + θw/ε)
/ (1 - θw/η) PF+ ωw
/ (1 - θw/η) V + (1 - ωw)
(1 - θr/η) / (1 + θr/ε)
PR
と書き換えられる。すると、ωw，θw，θr
の各値が(13)式により定められるが、このような交錯したパラメター制約下での(13)式の直接推計は難しい。そこで、代わりに
(14) PW = a PF+ b V + c PR
と書き換えて、a，bおよびcの値を推計し、
(15) ωw (1 + θw/ε)
/ (1 - θw/η) = a
(16) ωw / (1 - θw/η)
= b
(17) (1 - ωw) (1 - θr/η)
/ (1 + θr/ε) = c
を解くことにより、ωw，θw，θrの各値が一意に求められる（注１）
。
（注１） Azzam（1996）のモデルには6本の式に7つの未知のパラメーターが含まれ、識別不可能であった。
つぎに、酪農協対メーカーの関係を表す(9)式について、つぎの仮定を設ける。
(5) 一般に、日本のスーパーは乳業メーカーに対して圧倒的に強い垂直的パワーをもつと言われているので、ひとまずメーカー対スーパーの垂直的パワー・バランスを0:1と仮定し、現実の飲用牛乳卸売価格を市場の最低水準と見なすことは妥当であろう。よって、(9)式のPWUをPWに置き換える。
(6) λwとθwは、どちらもメーカーの垂直的パワー・パラメターであるため、λw=θwと仮定する。
(7) 飲用原料乳か飲用牛乳かに関わりなく、その需要の価格弾力性は、酪農協とメーカーいずれにとっても同一と仮定し、ηf=ηw≡ηと置き換える。ηの値はAzzamと同様、定数と仮定する。
(8) メーカーの限界費用MCwを、先の仮定(4)と同様の議論により、変動費単価Vに等しいと仮定する。
以上の仮定(5)〜(8)を(9)式に組み込むと、
(18) PF = ωｆ (PM + TC) / (1 - θf/η)
+ (1 - ωｆ) (PW - V) / (1 + θw/ε)
と書き換えられる。すると、ωｆ，θf，θwの直接推計は難しいため、代わりに
(19) PF = d (PM + TC) + e (PW - V)
と書き換えて、dおよびeの値を推計し、
(20) ωｆ / (1 - θf/η)
= d
(21) (1 - ωｆ) / (1 + θw/ε)
= e
を解く。ただし、これでは3つの未知のパラメターωｆ，θf，θwに対して2本の式しかないため、一意解を求められない。そこで、つぎの制約（定義域）の下で、解の範囲を求めることにする。
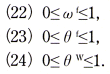
３．データ
1987〜2000年の年次データを用いて、OLS推計を行った。データの出所は、
PF：飲用乳価（円/リットル、農林水産省『農村物価賃金統計』の総合乳価、『牛乳乳製品統計』の加工原料乳基準取引価格、『食料需給表』の用途別生乳生産量を用いて算出した）、
PM：加工原料乳価（円/リットル、農林水産省『牛乳乳製品統計』加工原料乳基準取引価格）、
PW：飲用牛乳卸売価格（円/リットル、食品需給研究センター(2001)）、
PR：飲用牛乳小売価格（円/リットル、日経POS情報『NEEDS-SCAN』普通牛乳小売価格）、
TC：北海道から東京への飲用牛乳輸送費（円/リットル、ホクレンからの聞き取りにより1987年を25円、2002年を18円とし、その間で同額ずつ減少する系列を作成した）。
メーカーの変動費単価Vは、酪農乳業情報センター(2003)の調査によると、主に包材費、労務費および製品保管輸送費により構成されている。そこで、各費目の絶対金額に物価指数をかけ合わせ、V= 7.37PK + 7PL + 15.6PTとしてデータ系列を作成した。物価指数データの出所は、
PK：包材費指数（2000年=1、日本銀行『国内企業物価指数』紙製容器）、
PL：労務費指数（2000年=1、厚生労働省『毎月勤労統計調査』常用労働者30人以上の食料品製造業）、
PT：製品保管輸送費指数（2000年=1、日本銀行『企業向けサービス価格指数』道路貨物輸送サービス）、
各絶対金額は、2000年度平均単価（円/リットル、酪農乳業情報センター(2003)）を適用した。
供給の価格弾力性値eについては、Suzuki(2002)で計測された0.7175、需要の価格弾力性値hについては、Kinoshita et al.(近刊)で計測された0.21を適用した。
４．推計結果
(14)および(19)式の推計結果は、それぞれ
(25) PW = -0.0589 PF -0.0396 (7.37PK + 7PL + 15.6PT) + 0.9163 PR,
(-3.64) (-1.33) (75.22)
自由度調整済み決定係数 0.997, ダービン・ワトソン比 1.84.
(26) PF = 0.4968 (PM + TC) + 0.3924 (PW - 7.37PK - 7PL - 15.6PT),
(1.98) (2.40)
自由度調整済み決定係数 0.745, ダービン・ワトソン比 1.32.
ここで、係数推計値の下の( )内はt値である。ただし、(25)式には、系列相関修正のため、1階の自己回帰モデルを適用した。また、1995年および1998年に原因不明の大きな推計誤差が認められたため、各年のダミー変数を組み込んだ。(26)式も同様の理由で、1996年のダミー変数を組み込んだ。
(15)，(16)，(17)式により、ωw，θw，θrの各値は
(27) ωw = 0.0264,
(28) θw = 0.3501,
(29) θr = 0.0097,
と推計された。メーカー対スーパーの垂直的パワー・バランスωw : (1-ωw)は、0.0264 : 0.9736となり、ほぼ0 : 1でスーパーが完全優位である。一方、スーパー間の水平的競争度θr （=λr）は0.0097と、ほぼ0に近く、完全競争状態に近いのに対して、メーカーの水平的競争度θw （=λw）は0.3501であり、比較的高い。
(20)〜(24)式により、ωｆ，θf，θwの値がとりうる範囲は、
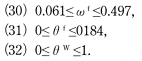
と推計された。酪農協対メーカーの垂直的パワー・バランスωｆ : (1-ωｆ)は、0.497:0.503から0.061:0.939の範囲となる。すなわち、酪農協とメーカーは、ほぼ対等か、酪農協が劣位であり、最小でほぼ0.1対0.9となる。酪農協間の水平的競争度θfは0.184以下であり、完全競争状態に近い。以上の結果を総括したのが図1である。
なお、(14)式から得られた推計値(27)〜(29)は、酪農協対メーカーの垂直的パワー・バランスを0:1とした仮定(1)に依拠しているが、推計値(30)は、この仮定(1)がほぼ妥当する場合もあることを実証している。一方、(19)式から得られた推計値(30)〜(32)は、メーカー対スーパーの垂直的パワー・バランスを0:1とした仮定(5)に依拠しているが、推計値(27)は、この仮定(5)が妥当であったことを実証している。
４．おわりに
以上のような形で農産物流通の各段階における垂直的パワー・バランスを実証した研究は、これまで国内にはなかった。また、実証分析によって得られた結果は、牛乳取引関係者の多くがもつ実感とも一致しており、興味深い。
ただし、垂直的パワー・バランスと水平的競争度との関係の理論的解釈について、まだ検討すべき問題も残っており、本稿の推計結果およびその解釈は暫定的なものと考える必要がある。一層の検討を加えた上で、「適正価格」についても、今後の研究で最終的な数値を提供したいと考えている。
|
図1 酪農協･メーカー･スーパー間の
垂直的パワーバランスと水平的競争度の推計結果 |
 |
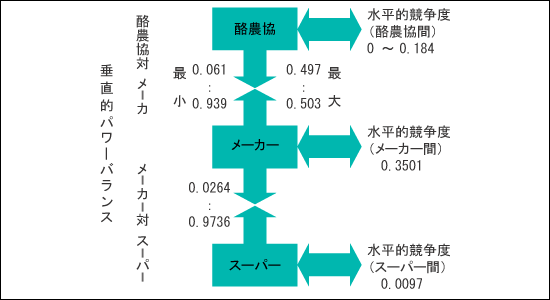| 注：垂直的パワーバランスは、0＝完全劣位、1＝完全優位。 水平的競争度は、0＝完全競争、1＝独占。 データ：酪農乳牛情報センター、食品需給研究センターなど。 |
＜引用文献＞
Azzam, A.M. (1996) Estimating the Degree of Dominance in a Bilateral Oligopoly.
Applied Economics Letters 3. pp.209-11.
酪農乳業情報センター (2003) 生乳取引ハンドブック2003.
鈴木宣弘 (1991) 推測的変動による不完全競争市場のモデル化と政策変更効果の計測−生乳市場を事例として−. 農業経済研究 63-1. pp.11-21.
鈴木宣弘 (2002) 寡占的フードシステムへの計量的接近. 農林統計協会.
Suzuki, N., J.E. Lenz and O.D. Forker (1993) A Conjectural Variations
Model of Reduced Japanese Milk Price Supports. American Journal of
Agricultural Economic 75. pp. 210-18.
食品需給研究センター (2001) 牛乳の価格動向調査.
Kinoshita, J., N. Suzuki, and H. M. Kaiser (近刊) An Economic Evaluation
of rbST Approval in Japan. Journal of Dairy Science.